Tree - 깊이 우선 탐색, 너비 우선 탐색, Binary Search Tree

Tree

Tree 자료 구조는 대표적인 비선형 구조의 자료 구조이다. 

비선형 자료구조란, 선형 구조가 아니라는 뜻.

 

선형 구조란, 자료 구조를 구성하는 데이터가 연속적으로 나열되어 있는 구조이다.

배열, 큐, 스택, 연결 리스트 등이 모두 해당된다.

 

반면, 트리는 비선형 구조이다. 

이름에서 알 수 있듯이, 자료가 하나의 root에서 시작해 가지치듯이 쭉쭉 확장되는 자료 구조이다.

대표적인 자료구조로 족보를 들 수가 있다.

Tree에 쓰이는 용어들도 족보(가계도)와 같은 용어가 많이 쓰인다.

그리고 윈도우의 파일 시스템도 대표적인 트리 구조의 예다. 

 

트리 구조는 상하 관계가 명확하기 때문에, 계층 구조를 구현하는 데 적합하다.

Tree 자료 구조는 기본적인 용어들이 많다.

 

우선 가장 맨 위에 있는 노드를 Root node라고 한다.

그리고 어떤 노드의 상위 노드를 Parent node(부모 노드), 하위 노드를 Child node(자식 노드)라고 한다.

CSS의 선택자와 개념이 비슷한데, DOM도 Tree 구조라서 그렇다.

 

Root node를 level 0이라고 했을 때, child node는 level 1, 그 child node는 level 2... 가 된다.

Tree의 Depth(깊이)는 가장 하위의 노드의 level이 될 것이다.

같은 level에 있는 node를 Sibling(형제 노드)라고 한다.

자식이 없는 딩크족 노드는 Leaf node라고 한다. 나무에 빗대어서 나뭇잎이라는 뜻으로 쓰이는 듯 하다.

 

마지막으로 node와 node가 연결되는 선을 Edge(간선)라고 한다.

 

만약 Tree를 프로그래밍 할 일이 있다면은, 위 용어를 잘 기억했다가 변수명으로 써먹으면 좋을 것이다.

Tree 탐색 기법

Tree는 비선형 구조인 만큼, 자료구조를 탐색하는 여러가지 방법이 있다.

일단은 크게 깊이 우선 탐색(DFS, Depth First Search)과 너비 우선 탐색(BFS, Breadth First Search)이 있다.

 

깊이 우선 탐색은 트리에서 깊이, 그러니까 수직적 방향으로 탐색을 실시하는 것이다.

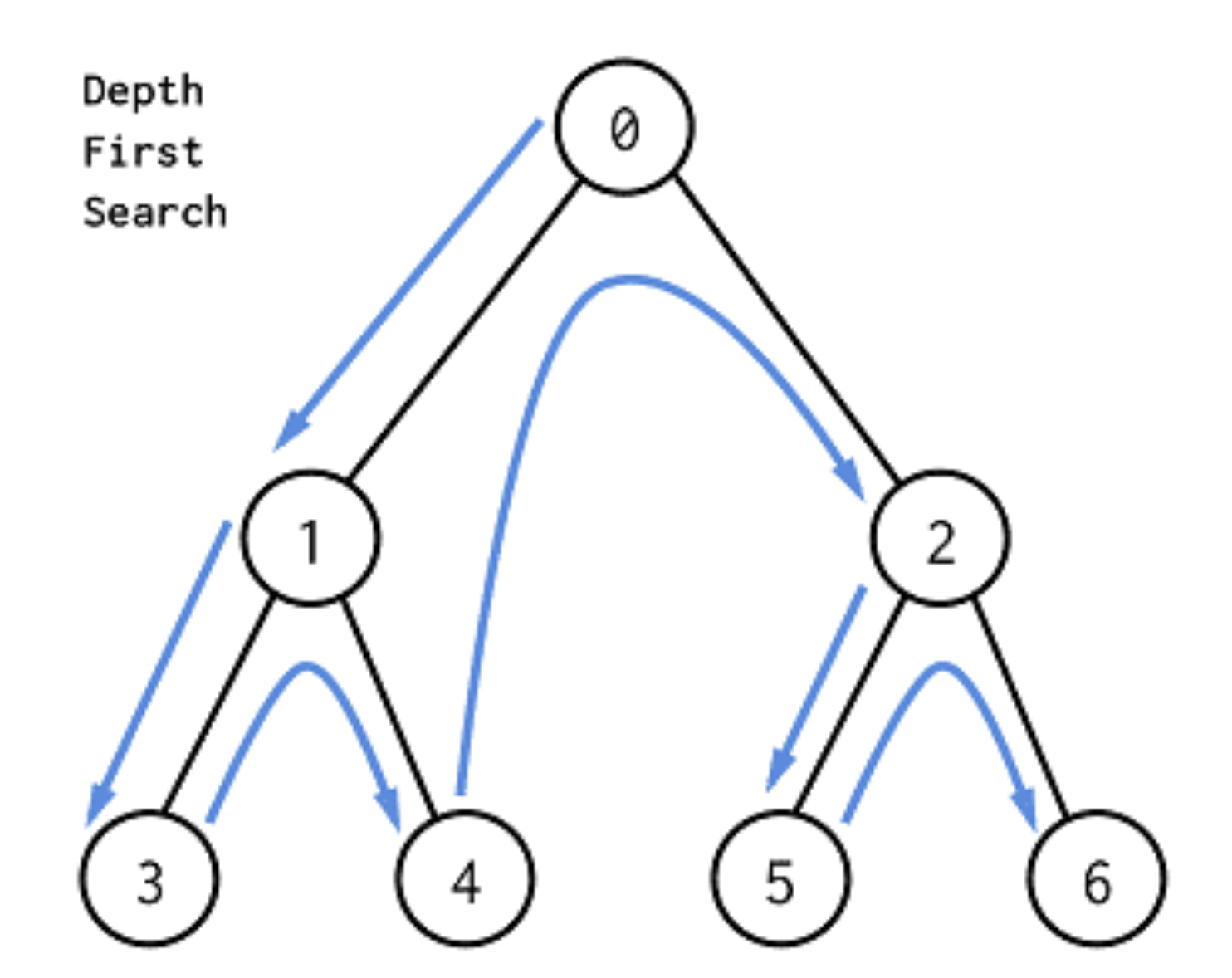
Root에서 시작해서 하나의 자식 노드를 모두 탐색하고, 그 다음 형제 노드를 탐색하게 된다.

 

DFS에서도 탐색하는 방법이 나뉘는데,

어떤 노드를 N, 그 자식 노드를 L, R이라고 가정해보자.

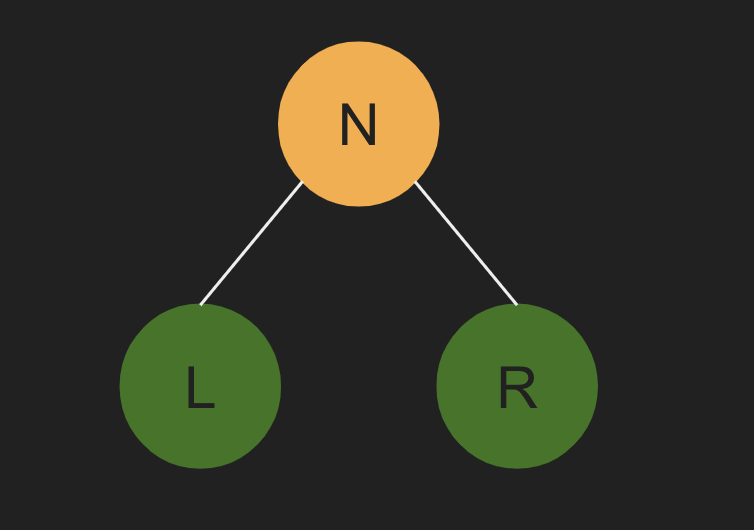
pre-order 방식은 N L R / post-order 방식은 L R N 

순으로 탐색하게 된다.

 

예제를 확인해보자.

pre-order 방식은 부모 노드를 가장 먼저 탐색한다.

0 → 1 → 3 → 4 → 2 → 5 → 6 순으로 진행한다.

 

조금 잘 이해가 되지 않는다면, 큰 덩어리로 나눠서 생각해보면 된다.

크게는 0 → 1 → 2 순으로 진행되는데, 1에서 또 자식 노드가 있으므로 1 → 3 → 4 식으로 탐색하게 된다.

0 → (1 → 3 → 4) → (2 → 5 → 6) 순으로 진행되는 것이다.

 

그 다음, post-order 방식은 부모 노드를 가장 마지막에 탐색한다.

3 → 4 → 1 → 5 → 6 → 2 → 0 순으로 진행한다.

마찬가지로, (3 → 4 → 1) → (5 → 6 → 2) → 0로 이해하면 더욱 편할 것이다.

 

탐색 시퀀스를 보면 알겠지만, 일종의 재귀적인 면이 있다.

그래서 재귀적으로 구현하는 경우가 많다.

 

그 다음 너비 우선 탐색(BFS)을 알아보자.

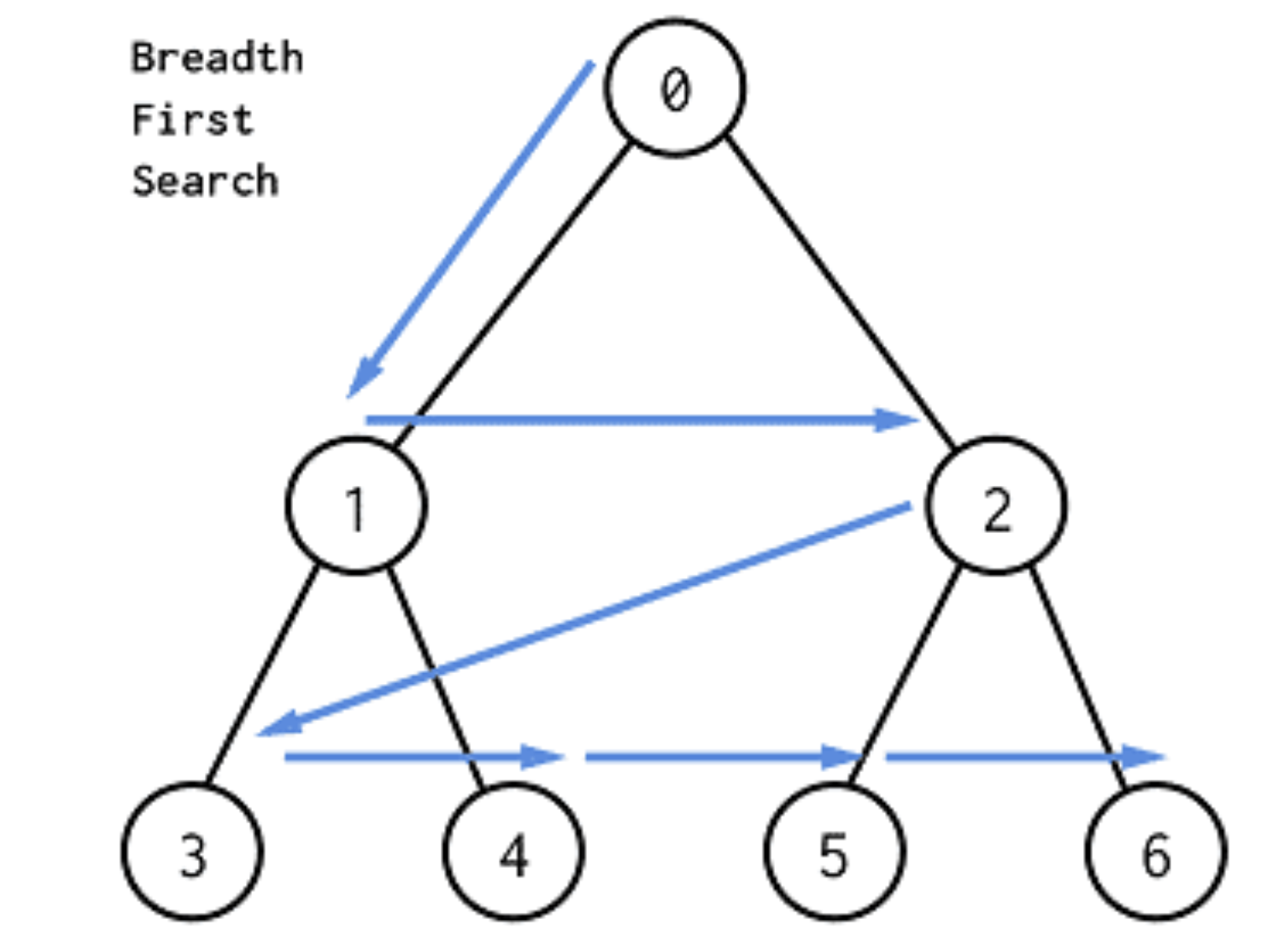
너비 우선 탐색은 반대로 횡적인 방향을 우선으로 탐색하는 것을 의미한다. 

깊이 우선 탐색과는 다르게, 재귀적인 구현이 쉽지는 않다.

 

주로 큐와 재귀를 이용해서 구현하게 된다.

그 과정을 한 번 살펴보자.

 

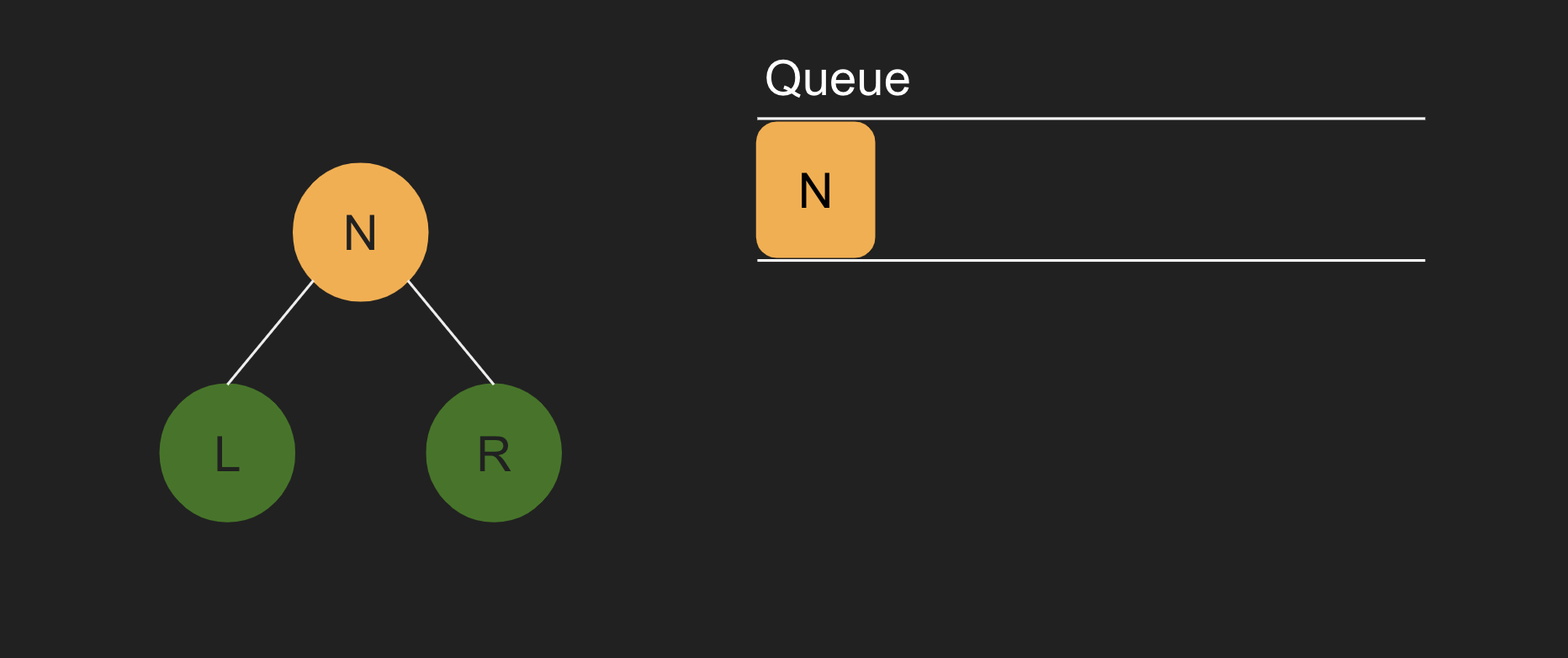
1. 우선 큐에 N이 들어간다.

2. N이 빠져나오면서, N을 검사한다.

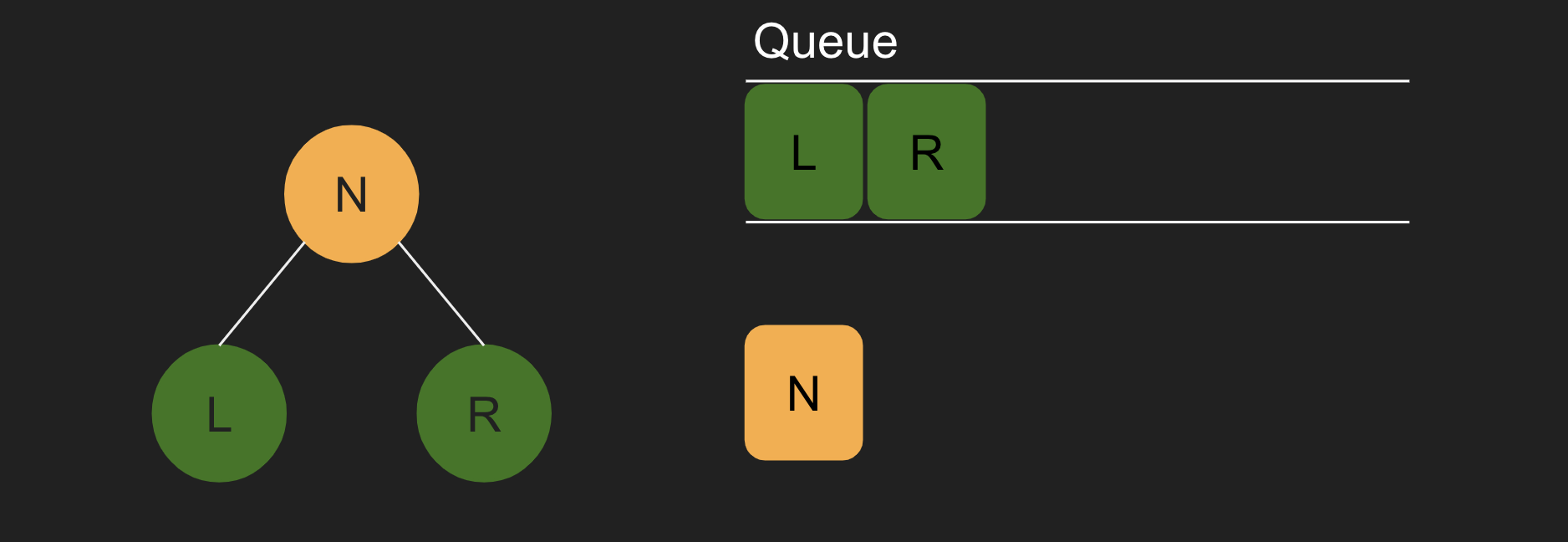
3. N에 있는 자식 노드(L과 R)를 큐에 넣는다.

4. L이 빠져나오면서, L을 검사한다. 자식 노드가 없으므로, 큐에는 아무것도 추가되지 않는다.

5. R이 빠져나오면서, R을 검사한다. 마찬가지로 자식 노드가 없으므로, 큐에는 아무것도 추가되지 않는다.

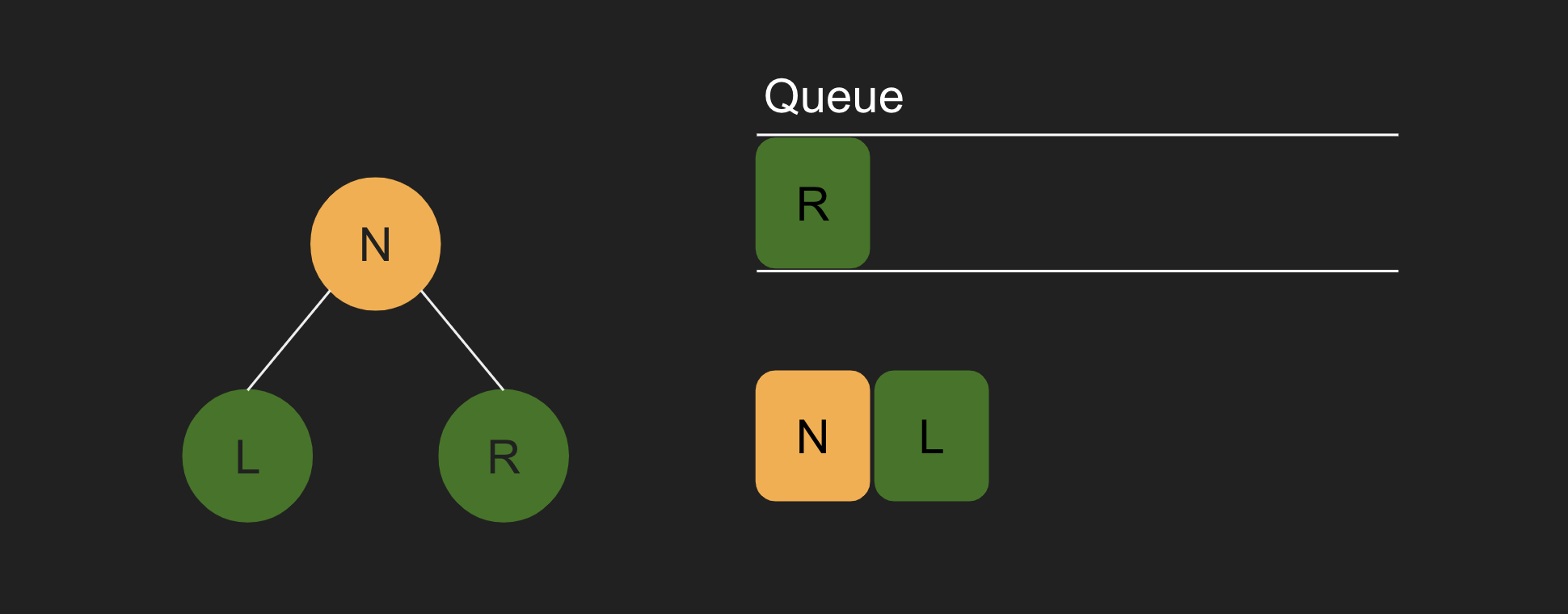
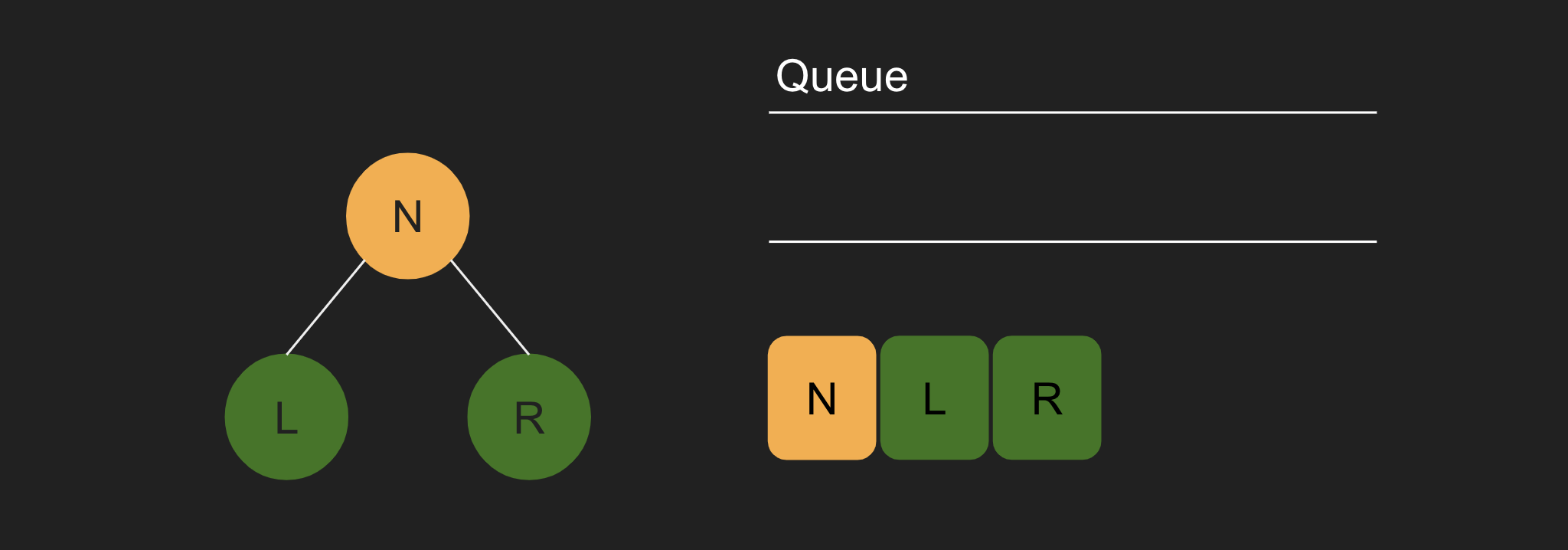
6. 큐가 완전히 비어있게 되면, 탐색이 종료된다.

 

DFS가 탐색하는 동시에 바로 검사를 하는 것과 다르게, BFS는 형제 노드를 먼저 검사하기 위해 자식 노드를 큐에 담는 식으로 진행된다.

저기서 깊이가 더 깊은 Tree라고 해도 저 방식이 재귀적으로 이루어지기 때문에, 잘 동작하게 된다.

 

Binary Search Tree(이진 탐색 트리)

트리에서도, 트리를 응용한 여러 자료구조들이 굉장히 많이 있다.

그중에서도 대표적인 자료구조가 Binary Search Tree(이진 탐색 트리)인데, 이름에서도 알 수 있듯이 탐색에 특화되어있는 자료구조이다.

 

이진 탐색 트리의 대표적인 두 가지 원칙? 정의가 있는데,

첫 번째, 하나의 노드는 0 ~ 2개의 자식 노드를 가진다. 최대 2개만을 자식노드로 가질 수가 있는 것이다.

두 번째, 모든 노드는 좌측이 부모 노드보다 작은 값. 우측이 부모노드보다 큰 값을 가진다.

 

이런 구조로 인해서, 이진 탐색 트리는 남다른 검색 속도를 가질 수 있다.

 

Binary Tree라는 것도 있는데, Binary Search Tree와는 다른 자료 구조이다.

Binary Tree는 Binary Search Tree의 첫 번째 원칙만을 가지는 자료 구조다.

 

이진 탐색 트리도 트리와 탐색기법이 동일한데, 깊이 우선 탐색에서 pre-order와 post-order 이외에 in-order 방식이 있다.

아까처럼 N, L, R 노드가 있을 때, L, N, R 순으로 탐색하는 방식이다.

Tree 탐색 기법의 예시에서, 3 → 1 → 4 → 0 → 5 → 2 → 6으로 실행하게 될 것이다.

Binary Search Tree의 시간 복잡도

Binary Search Time에서 시간 복잡도는 O(log n)이다. 

O(log n)은, 지금까지 O(1), O(n)과 같은 시간복잡도와는 달리 직관적인 개념은 아니다.

 

예시를 통해서 시간 복잡도를 한 번 계산해보자.

 

크기가 16인 Binary Search Tree가 있다.

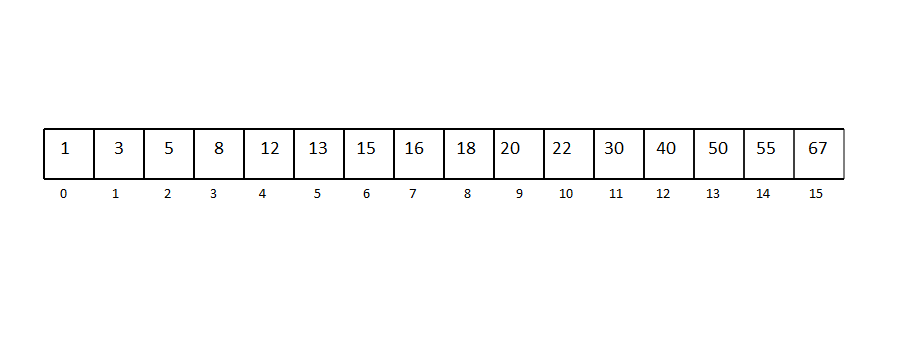
이해를 위해서 배열의 구조로 나타내었다.

여기에서 13을 탐색하는 경우를 생각해보자.

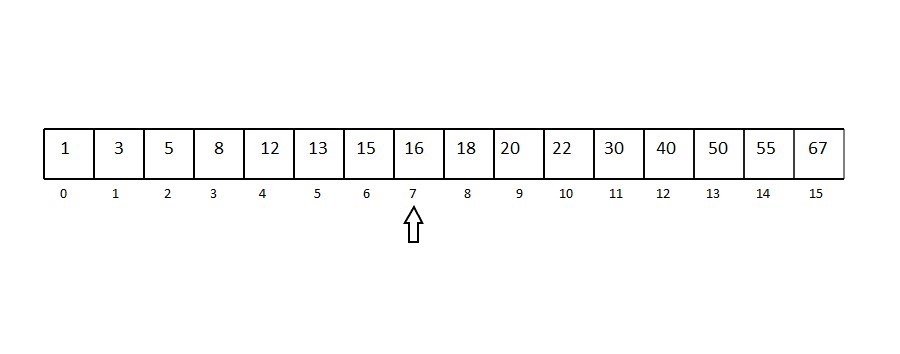
우선 중간 node인 16으로 가보자. 13은 16보다 작다.

그러므로 총 16개의 노드 중에서, 절반인 8개의 노드를 탐색하면 된다.

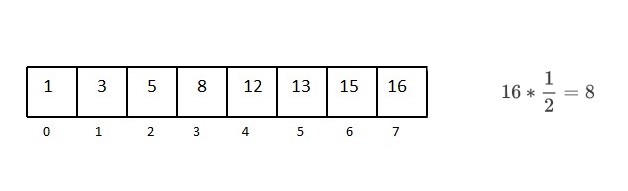
8개의 노드 중에서, 중간인 8로 가보자. 13은 8보다는 크다.

8개의 노드에서, 절반인 4개의 노드를 탐색하면 된다.

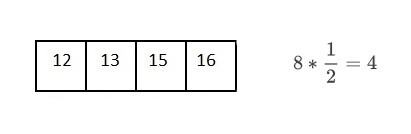
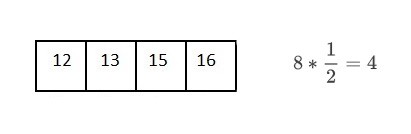
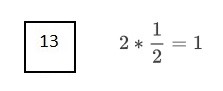
이렇게 1/2, 1/2... 해나가다보면 13 하나의 노드만이 남게 된다.

이를 수식으로 나타내면 다음과 같다.

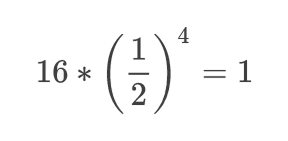
크기가 16인 이진 탐색 트리는, 절반을 탐색하는 4번의 동작을 거쳐서 하나의 노드를 찾게 되는 것이다.

그리고 이를 크기가 n인 이진 탐색 트리로 나타내보자. 

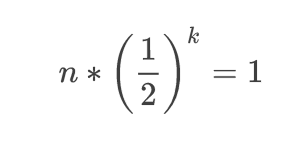
크기가 n인 이진 탐색 트리는, (1/2)^k승을 통해 1이 되는 수식으로 나타낼 수 있다.

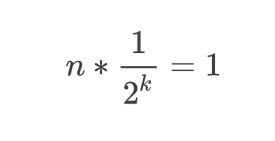
이 수식은 다음과 같이 풀어낼 수 있다.

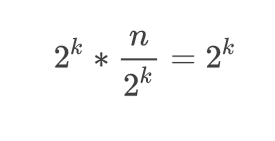
양 쪽에 2^k를 곱해주었다.

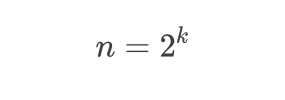
그리고 위 수식을 다음과 같이 나타낼 수 있다.

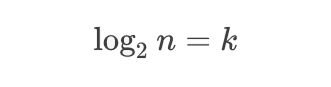
그래서 k를 마침내, log2 n으로 나타낼 수 있게 되었다.

여기서는 탐색을 예시로 들었지만, 삽입이나 삭제의 경우에도 동일하게 생각할 수가 있다.

 

하지만 최악의 경우에는 O(n)의 시간 복잡도를 가질 수도 있다.

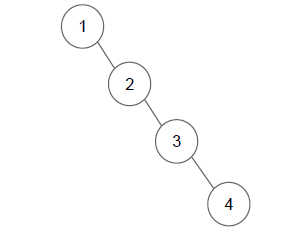
이렇게 기형적인 이진 탐색 트리가 있다면, 모든 노드를 탐색해야 하므로 O(n)의 시간 복잡도를 가질 수도 있다.

 

여기에서 기인한 여러가지 파생 트리들이 있는데, 대표적으로 AVL Tree와 Red Black Tree와 같은 것이 있다.

이런 트리들은 self-balancing을 통해서 노드들이 치우치지 않도록 구성된다.